-
- Downloads
Documentation: Doxygen page about interference functions (text and figures),...
Documentation: Doxygen page about interference functions (text and figures), UserManual (modifications of ff.tex and interferences.tex)
Showing
- Core/Algorithms/inc/SimulationParameters.h 1 addition, 0 deletionsCore/Algorithms/inc/SimulationParameters.h
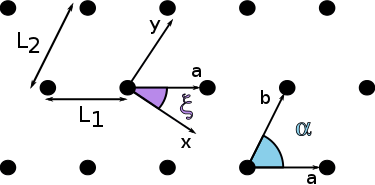
- Doc/Doxygen/Figures/2Dlattice.png 0 additions, 0 deletionsDoc/Doxygen/Figures/2Dlattice.png
- Doc/Doxygen/Figures/grating3D.png 0 additions, 0 deletionsDoc/Doxygen/Figures/grating3D.png
- Doc/Doxygen/defgroups.doc 101 additions, 0 deletionsDoc/Doxygen/defgroups.doc
- Doc/UserManual/ff.tex 219 additions, 423 deletionsDoc/UserManual/ff.tex
- Doc/UserManual/interferences.tex 81 additions, 243 deletionsDoc/UserManual/interferences.tex
Doc/Doxygen/Figures/2Dlattice.png
0 → 100644
14.1 KiB
Doc/Doxygen/Figures/grating3D.png
0 → 100644
124 KiB
This diff is collapsed.
This diff is collapsed.